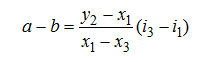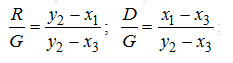Бродянский В.М., Калинина Е.И.
Разделение газовых смесей
3-2. Непрерывные испарение и конденсация
бинарной смеси при Т < Tос
3-2-1. Непрерывное испарение (Ж→П)
Рассмотрим этот процесс сначала в общем виде, без учета характера взаимодействия пара и жидкости. (Схема показана на рис. 3-1.) Точкам 1 – входа смеси, 2 – выхода пара и 3 – выхода жидкости соответствуют величины энтальпий i и концентраций S. [В дальнейшем концентрация пара по легкокипящему компоненту обозначается y, концентрация жидкости - х] Общее количество подводимого тепла – Q+.
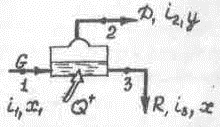
Рис. 3-1
Количественные показатели процесса можно определить из трех уравнений:
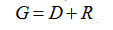 (3-1) (3-1)
– общий материальный баланс;
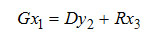 (3-2) (3-2)
– баланс по легкокипящему компоненту;
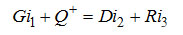 (3-3) (3-3)
- энергетический баланс.
Расчеты разделительных аппаратов удобно проводить на единицу получаемого продукта или в других удельных величинах.
Количество подводимой смеси G и отводимой жидкости на единицу получаемого пара определяются по формулам, выведенным из (3-1) и (3-2),
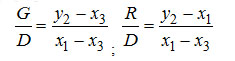
Уравнение энергетического баланса в удельных величинах на единицу D можно записать следующим образом:
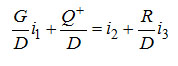
Если Q+/D обозначить удельнай величиной qD+ и вместо G/D и R/D подставить их значения, то уравнение примет вид
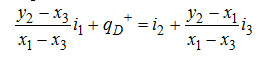 . .
Отсюда удельный расход тепла в испарителе равен
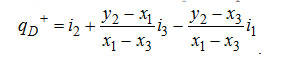
Если преобразовать разность y2-x3=(y2-x1)+(x1-x3), как и отношения разностей, то выражение для qD+ может быть записано в окончательном виде так:
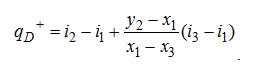 (3-4) (3-4)
Величина qD+ может быть определена и графическим построением в i-диаграмме (рис.3-2). Для этого точки 1 и 3 соединяются прямой линией, которая отсекает на ординате ξ2 отрезок 2-в, равный величине qD+ . Это построение справедливо и для случая, когда точка 1 не лежит на кривой кипения (т.е. жидкость подается в аппарат при Ткип). Естественно, что в этом случае будет больше.
Отрезок 2-в состоит из отрезка 2-а, величина которого равна разности энтальпий отрезка а-в. Из рассмотрения двух подобных треугольников 3o1 и 1ав величина отрезка а-в может быть записана так:
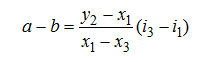
Следовательно, отрезок 2-а представляет собой два первых члена выражения для qD+ , а отрезок а-в – последний член, Значение qD+ может быть определено через энтальпии точек 2 и в qD+ =i2-ib
Аналогично, из соотношения, выведенного выше из балансовых уравнений, могут быть получены материальные и энергетические характеристики процесса непрерывного испарения, отнесенные к единице подаваемой смеси
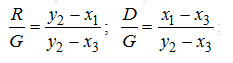
Величина qD+ может быть найдена графически на i, ξ диаграмме, как отрезок 1-4 ординаты х1,(рис. 3-2).
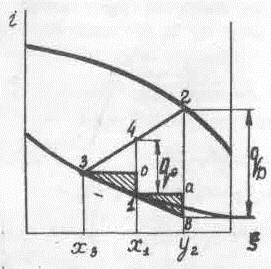
Рис. 3-2
Таким образом, из балансовых уравнений, характеризующих процесс, выявляются связи между его параметрами в аналитической и графической формах.
Рассмотрим в общем виде влияние величины тепловой нагрузки, отнесенной к единице подаваемой смеси, на количество и концентрацию продуктов при непрерывном испарении (рис. 3-3).
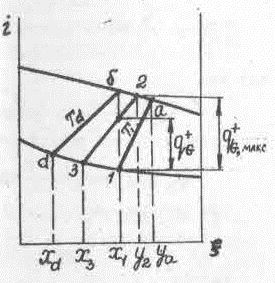
Рис. 3-3
При значениях qD+ , близких к нулю ( qD+→0), испарения жидкости практически не происходит, и отводимая жидкость имеет тот же состав, что и поступающая на испарение, т.е. .
Количество пара, образующегося при этих значениях qD+ , также стремится к нулю; его температура практически равна температуре поступающей жидкости (Ta=T1) и концентрация близка к равновесной относительно этой жидкости y2→ya – это максимально возможная концентрация пара в процессе при количестве его, близком к нулю.
При больших значениях qD+ , близких к обеспечивающему практически полное испарение поступающей жидкости, вся жидкость испарится, и концентрация полученного пара будет равна концентрации исходной смеси, т.е. yb~x1 .
В этих условиях концентрация пара приближается к минимальной при максимально возможном его количестве, равном в пределе G.
Соответственно доля жидкости, которая может отводиться из испарителя при qD+ → qD+макс близка к нулю, состав этой жидкости равновесен получаемому пару и характеризуется точкой d на рис. 3-3. Температуры полученных продуктов при этом будут равны между собой и больше температуры исходной смеси (Tb=Td>Т1).
Таким образом, при крайних значениях qD+ непрерывное испарение либо не проводится (qD+ =0), либо превращается в процесс полного испарения жидкости (qD+ = qD+макс ). При этом выявляются пределы изменения концентрации легкокипящего компонента в получаемых продуктах: паре ya>y2>yb и жидкости x1>x3>xd .
Для полной информации о процессе необходимо учесть относительное направление движения жидкости и пара, что существенно влияет на концентрацию продуктов.
Проведем для оценки этого влияния сравнение противоточного и прямоточного варианта непрерывного испарения в идеальных условиях.
[Под идеальными условиями в рассматриваемом случае понимаются такие, когда между какими-либо потоками пара и жидкости на границе аппарата в результате тепломассообмена устанавливается равновесие. Это означает равенство температур и химических потенциалов пара и жидкости на входе или выходе из аппарата; их составы соответствуют равновесным. Идеальные условии соответствуют либо бесконечно большому времени, либо бесконечно большой поверхности контакта фаз.]
При противотоке (рис.3-4 а) пар движется навстречу жидкости, находясь с ней в постоянном контакте. Выходящий из аппарата пар встречается с исходной жидкостью. При идеальных условиях проведения процесса пар D (точка 2а) будет равновесен жидкости G (точка 1) и Т2a → T1.
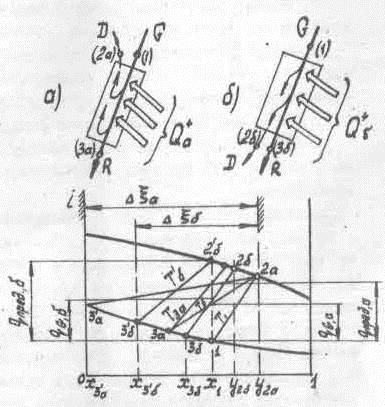
Рис. 3-4
Состав жидкости R (положение точки 3а на диаграмме L, ξ) определяется величиной qG+a . Чем больше количество подведенного тепла, тем меньше концентрация и количество получаемой жидкости.
Температура выходящей жидкости всегда выше температуры исходной жидкости смеси G и отводимого пара D, т.е. T3a > T2a → T1 .
При определенном значении qG+a концентрация жидкости может достигнуть ξб = x3a = 0 , т.е. в результате процесса получится чистый тяжелокипящий компонент. Это значение qG+a можно назвать предельным и обозначить q+пред, a
Таким образом, интервал возможных концентраций получаемых продуктов находится между xmin,a = x3a → 0 (при q+пред, a ) и y1 → y2a , равновесной х1. На рис.3-4 он обозначен величиной Δ ξa (в i, ξ диаграмме).
При прямотоке (рис.3-4 б) направления движения пара и жидкости совпадают. На выходе из аппарата при идеальных условиях получаемые пар D и жидкость R находятся в равновесии и T2в → T3б (изотерма Tb на рис. 3-4).
Как видно из диаграммы на рис. 3-4, в зависимости от количества подведенного тепла изотерма, соединяющая точки 3б и 2б в идеальном процессе, может достигать двух крайних положений. При q+пред, a получаемая жидкость R будет иметь концентрацию xmin,б = x3б , а при qG,б → 0 пар D будет характеризоваться составом yмакс → 2а . За пределы этого интервала, обозначенного Δξб (показан штрихом), составы получаемых продуктов выйти не могут. Во всех случаях при q+G≠ 0 температуры получаемых продуктов T3 и T2 больше, чем T1.
Сопоставляя процессы непрерывного испарения в противоточном и прямоточном вариантах, можно сделать следующие выводы.
1. Полное разделение смеси с получением обоих чистых компонентов путем непрерывного испарения невозможно.
2. В противоточном варианте испарения возможно получение чистого тяжелокипящего компонента. Однако коэффициент извлечения этого компонента не может достичь единицы, т.к. часть его всегда отводится с паром. [Коэффициент извлечения компонента ηизвл определяется отношением количества G" данного компонента к количеству его G' в исходной смеси ηизвл = G"/ G'.]
В прямоточном варианте оба продукта могут быть получены только в виде фракций, обогащенных одним или другим компонентом.
3. Температуры T2 и T3 продуктов разделения всегда выше, чем исходной смеси T1. Это означает, что минимальная потеря при теплообмене в процессе испарения соответствует условиям подогрева при переменной температуре в интервале от T1+ΔT до T3+ΔT. Следовательно, поток греющего вещества должен быть либо однофазным, либо двухфазным (пар + жидкость), но не однокомпонентным; в противном случае его температура будет неизменной. Начальная температура греющего потока должна быть возможно ближе к Tb, а конечная – к T1.
Следующая страница: Непрерывная конденсация
| 

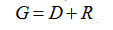 (3-1)
(3-1)
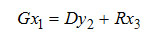 (3-2)
(3-2)
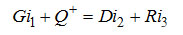 (3-3)
(3-3)
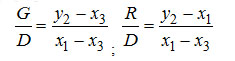
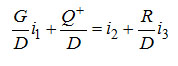
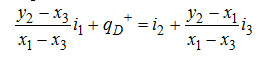 .
.
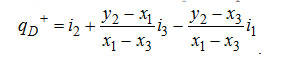
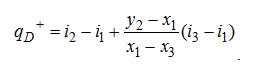 (3-4)
(3-4)