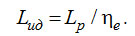|
| Испарение и конденсация |
Пленочное кипение |
Сверхтекучий гелий |
Эксперименты | События | Библиотека |
Испарение и конденсацияПленочное кипениеСверхтекучий гелийЭксперименты События и мероприятияБиблиотека• История холода• Элементы физической кинетики• Разделение газовых смесей• Методические указания. Анализ криогенных установок• Оборудование гелиевого ожижителя Г-45• Методические указания. К практическим занятиям в криоцентре• Криогенные трубопроводы• Хранение и транпорт ожиженных газов• Основы методики проектирования криогенных установок• Вспомогательное оборудование криогенных установок• Расчет и оптимизация схем криогенных установок• Расчет низкотемпературных установок• Методика расчета схем криогенных установок (рефрижераторы и ожижители)• Методика расчета схем криогенных установок (рефрижераторы с нестационарными потоками)• Характеристики криогенных систем при работе на смесях• Механические свойства твердых тел при низких температурах• Людвиг Больцман. Лекции по теории газовСправочные данные БольцманиадаХейке Камерлинг-ОннесКриогениус |
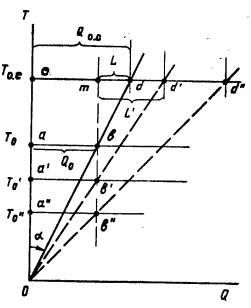
Бродянский В.М. От твердой воды до жидкого гелия (история холода)Абсолютная температурная шкалаЦикл Карно не только дает идеальную модель холодильного процесса; он позволяет и количественно определить, сколько работы нужно затратить, чтобы отвести теплоту Qо на низком температурном уровне То<То.с при заданной температуре Tо.с. Более того, он позволяет, как показал Томсон-Кельвин, и установить абсолютную температурную шкалу. Графическое построение, позволяющее наглядно проиллюстрировать все связанные с этими вопросами количественные соотношения, показано на рис. 2.9.
Проведем на графике две горизонтальные линии: одну верхнюю – на уровне температуры окружающей среды То.с, и другую, нижнюю – на уровне Т0 охлаждаемого объекта. Тогда на последней горизонтали можно отложить отрезок, равный количеству теплоты Qо. Если теперь провести через начало координат и точку b прямую (луч), то она отсечет на линии То.с отрезок сd. Он в том же масштабе покажет количество теплоты Qос, которое в результате действия цикла будет отдано окружающую среду. Отрезок md на этой прямой будет соответствовать затраченной в цикле работе L, поскольку по закону сохранения энергии
Из этого же построения следует (поскольку треугольники 0cd и 0ab подобны), что
Это важнейшее следствие анализа цикла Карно позволяет, как показал Кельвин, подойти к определению абсолютной шкалы температур. Действительно, отношение двух количеств теплоты (которое можно вычислить по свойствам рабочего тела, найденным экспериментально) равно отношению их температур по абсолютной шкале, которая не связана со свойствами какого-либо термометрического вещества. Нужно только присвоить какому-либо одному значению температуры численное значение в градусах, а другое, соответствующее самой низшей возможной точке – абсолютному нулю, принять за нуль. Такая шкала была официально установлена только через сто с лишним лет после выхода статьи Томсона-Кельвина (1849 г.). Это произошло в 1954 г. на IX Генеральной международной конференции по мерам и весам. В качестве опорной точки шкалы была принята температура тройной точки воды; здесь одновременно могут существовать лед, пар и жидкая вода. Ей присвоено значение 273,16K9. Начальная точка – 0K соответствует абсолютному нулю. Чтобы пересчитать градусы шкалы Цельсия в градусы шкалы Кельвина, надо прибавить к ним 273,15 (K=°С+273,15). График, показанный на рис. 2.9, обладает еще одним замечательным свойством: он наглядно показывает, чем определяется и как растет необходимая затрата работы L по мере понижения температуры Т0. Из него видно, что из подобия треугольников mdb и аb0 следует:
Эта формула была названа именем Карно. Если мы должны произвести то же количество холода Q0, но не при температуре Т0, а при другой, более низкой, например при T'0<Т0, и все остальные условия остаются прежними, то можно воспользоваться не только (2.6), но и найти затрату работы графически. Проведем на графике новую изотерму Т'0 и отложим на ней то же количество теплоты Q0. Получим точку b' расположенную под точкой b. Если теперь повторить то же построение, что и для Т0, проведя из начала координат луч через точку b', то на линии То.с получим больший отрезок md', соответствующий необходимой затрате работы L'. Видно, что чем ниже Т0, тем больше нужно затратить работы на отвод теплоты Q0; тем холод энергетически дороже. Очевидно, что при дальнейшем понижении Т0 работа L будет возрастать все быстрее, а по мере приближения к абсолютному нулю (Т=0) L→∞. Если перевести эту зависимость на язык цифр и принять Q0=1 Дж и Т0=293K (-20°С), то значение L в зависимости от Т0 будет выглядеть так, как показано в табл. 2.1. Таблица 2.1. Зависимость L от T0.
* Это значение соответствует самой низкой температуре, использованной Фарадеем (-110°С). Из таблицы 2.1 видно, что вплоть до температуры Т0=146,5K необходимая затрата работы L не превышает количества получаемого холода Q0. Другими словами, получение такого холода не требует очень больших энергетических затрат. Но дальше, чем ниже Т0, тем необходимая затрата работы растет все быстрее: на уровне температуры, равной, например, 50K, она уже превышает количество получаемого холода более чем в 4 раза. При температуре ниже 25K это соотношение10 доходит до десятков, а при еще более низкой температуре – до сотен и тысяч... Из табл. 2.1 видно, что уровень энергетических затрат на получение холода, при котором Фарадей ожижал "непостоянные" газы, "стоил" в единицах работы намного меньше, чем тот, с которым встретились его продолжатели, готовящиеся ожижить "постоянные" газы. Следует также учесть, что цифры в таблице относятся только к идеальным процессам; в реальных условиях получение холода связано с различными потерями11, которые тем больше, чем ниже температура. Они учитываются КПД соответствующих охлаждающих устройств. Значение этих КПД ?е меняется в пределах от 0,4 для крупных установок до 0,1 и ниже – для малых. Поэтому реальный расход работы Lр оказывается намного выше, чем в идеальном случае:
Работами С. Карно, В. Кельвина и Р. Клаузиуса было установлено, что абсолютный нуль температур находится по шкале Цельсия на уровне -273,15°С. Это позволило создать абсолютную шкалу температур (шкалу Кельвина), градусы (Т) которой те же, что и в шкале Цельсия (t), но их отсчет начинается с абсолютного нуля. Следовательно12, температура в °С равна температуре в K минус 273,15. М. Фарадей достиг -110°С, т.е. 163K; на пути к абсолютному нулю осталось пройти "всего" 163 градуса. Из табл. 2.1 можно видеть, насколько труднее с каждым шагом двигаться вниз. Поэтому чем ниже температура, тем чаще приходится вспоминать изречение Ф. Бэкона: "Природа с трудом дает нам холод". Однако получать его все же удавалось, вырывая с колоссальным трудом каждый участок на "пути к абсолютному холоду". Ведь тот же Бэкон сказал и другую, тоже вошедшую в историю, но намного более знаменитую фразу: "Знание – сила" (Knowledge is Power). Чтобы покорить и ожижить хотя бы один из "постоянных" газов, нужно было найти какой-то новый метод понижения температуры, позволяющий оторваться от фарадеевского рубежа хотя бы еще на несколько десятков градусов вниз. Следующая страница: 2.3. Новые способы охлаждения
|
|
Испарение и конденсация
Пленочное кипение
Сверхтекучий гелий
Эксперименты События Библиотека Справочники Больцманиада Камерлинг-Оннес Криогениус |
|
© Криофизика.рф 2006-2021. Молекулярно-кинетическая теория. Научные публикации. Испарение и конденсация. Плёночное кипение. Сверхтекучий гелий. |
о проекте условия использования |
контакты карта сайта |
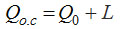 (2.4)
(2.4)
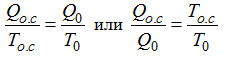 (2.5)
(2.5)
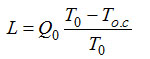 (2.6)
(2.6)